1. 从傅里叶变换到拉普拉斯变换
1.1 傅里叶变换的局限
傅里叶变换的公式:
$$ \begin{aligned} F(\omega) &= \int_{-\infin}^{\infin}{f(t) e^{-j\omega t} dt} \end{aligned} $$
其中的指数部分可以写为:
$$ e^{-jwt}=\cos{wt}-j\sin{wt} $$
但是对于函数比如 $f(t) = t^2$ 会发现根本积分不了,因为在无穷范围内积分的结果是无穷。
经典的傅里叶变换(非广义定义)通常要求 绝对可积条件:
$$ \int_{-\infin}^{\infin} |f(t)| dt < \infin $$
在工程中有一些方法可以处理这种不收敛的函数:
- 加窗:只在有限区间内考虑函数
- 专用拉普拉斯变换:拉普拉斯变换能处理发散情况,条件比傅里叶变换宽松。
那么如果还是希望能够分析这种函数,一个可行的方式是乘以某个指数函数,让它可以重新变成一个可积的函数。
这里只考虑积分正半部分,拉普拉斯变换通常只考虑正半部分。
有:
$$ \int_{0}^{\infin}{e^{-3 t} t^2 dt} = \frac{2}{27} $$
满足 绝对可积条件 。
如果我们将这个指数部分定义为 $\sigma$,定义 $s = \sigma + j\omega$,指数部分可以表述为
$$ e^{-\sigma t}e^{-j\omega t} = e^{-(\sigma + j\omega)t} = e^{-st} $$
这就引出了下面的拉普拉斯变换。
换句话说,傅里叶变换是拉普拉斯变换在 $\sigma = 0$ 时的特殊形式。
1.2 拉普拉斯变换
拉普拉斯变换(又称为拉式变换)是将时间域函数 $f(t)$(通常是 $t \ge 0$ 的信号或函数)映射到复频域函数 $F(s)$ 的一种方法,公式为:
$$ F(s) = \mathcal{L}{f(t)} = \int_{-\infin}^{\infin} f(t) e^{-st} dt $$
其中:
- $t$ 是时间变量。
- $s$ 是复频域变量,通常写作 $s = \sigma + j\omega$。
- $F(s)$ 是 $f(t)$ 的拉普拉斯变换。
这里的符号 $\mathcal{L}(f(t))$ 表示对 $f(t)$ 做拉普拉斯变换。
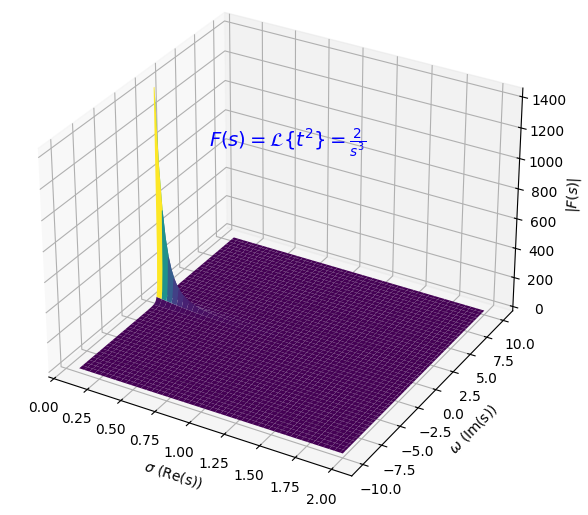
如果把 $t^2 (t>0)$ 频域打印出来,高度用 $F(s)$ 的幅度表示(相位在这里确实也不关键),可以得到一张复平面上拉普拉斯变换的幅值图:
拉普拉斯反变换:$F(s) \to f(t)$
$$ f(t) = \frac{1}{2\pi j} \int_{\gamma - j\infin}^{\gamma + j\infin} F(s) e^{st} ds $$
其中
- $\gamma$ 是实轴上一个常数,使积分路径在 $F(s)$ 的所有奇点右侧
- $s = \sigma + j\omega$
这里补充说明下,奇点是指 $F(s)$ 不存在或者发散的点,比如 $F(s)=\frac{2}{s^3}$ 的奇点是 $s = 0$。“右侧”意思是选一个实数 $\gamma$,使得这条垂直线 $s = \gamma + j\omega$ 位于所有奇点的右边,这样积分路径经过的地方,$F(s)e^{st}$ 在积分方向上是收敛的(假定原本积分是 t > 0),如果路径穿过奇点,积分会发散或者不满足公式要求。
1.3 单边拉普拉斯变换
工程领域,一般默认拉氏变换会对原函数先乘以阶跃函数再变换,阶跃函数是:
$$ u(t)= \begin{cases} &1, & t \ge 0\\ &0, & t \lt 0 \end{cases} $$
所以积分只需要在 $[0, +\infin]$ 之间进行积分,这被称为 单边拉普拉斯变换。
首先仔细推导一下 $f(x) = 1$ 的拉普拉斯变换。
拉普拉斯变换的定义是:
$$ \mathcal{L}{f(t)} = F(s) = \int_0^{\infin} f(t) e^{-st} dt $$
这里 $f(t) = 1$,所以:
$$ \mathcal{L}{1} = \int_0^{\infin} 1 \cdot e^{-st} dt = \int_0^{\infin} e^{-st} dt $$
这个积分可以直接计算:
$$ \int_0^{\infin} e^{-st} dt = \left[ -\frac{1}{s} e^{-st} \right]_0^{\infin} $$
当 $\Re(s) > 0$ 且 $t \to \infin$ 时,$e^{-st} \to 0$,所以:
$$ \int_0^{\infin} e^{-st} dt = lim_{t \to \infin}{(-\frac{1}{s} e^{-st})} - (-\frac{1}{s} e^{-s \cdot 0}) = 0 - \left(-\frac{1}{s}\right) = \frac{1}{s} $$
结论:
$$ \boxed{\mathcal{L}{1} = \frac{1}{s}, \quad \Re(s) > 0} $$
实际上我们并不需要一个个算,多数情况直接查表即可:
| 时域 $f(t)$ | 频域 $F(s)$ |
|---|---|
| $u(t)$ | $\frac{1}{s}$ |
| $u(t)e^{-at}$ | $\frac{1}{s+a}$ |
| $t u(t)$ | $\frac{1}{s^2}$ |
| $u(t) \sin \omega t$ | $\frac{\omega}{s^2 + \omega^2}$ |
| $u(t) \cos \omega t$ | $\frac{s}{s^2 + \omega^2}$ |
| $u(t)e^{-at} \sin \omega t$ | $\frac{\omega}{(s+a)^2 + \omega^2}$ |
| $u(t)e^{-at} \cos \omega t$ | $\frac{s+a}{(s+a)^2 + \omega^2}$ |
然后利用拉普拉斯变换的一些特性来求解。
1.4 积分特性:变上限积分的频域
$$ \mathcal{L} \left( \int_0^t{f(\tau)d\tau} \right) = \frac{F(s)}{s} $$
证明如下:
定义
$$ g(t) = \int_0^t f(\tau) d\tau $$
根据拉普拉斯定义:
$$ \mathcal{L}{g(t)} = \int_0^\infin g(t) e^{-st} dt = \int_0^\infin \left( \int_0^t f(\tau) d\tau \right) e^{-st} dt $$
交换积分顺序
$$ \int_0^\infin \left( \int_0^t f(\tau) d\tau \right) e^{-st} dt = \int_0^\infin f(\tau) \left( \int_\tau^\infin e^{-st} dt \right) d\tau $$
计算内层积分
$$ \int_\tau^\infin e^{-st} dt = \left[ \frac{-1}{s} e^{-st} \right]_{t=\tau}^{t=\infin} = \frac{e^{-s\tau}}{s} $$
回代外层积分
$$ \mathcal{L}{g(t)} = \int_0^\infin f(\tau) \frac{e^{-s\tau}}{s} d\tau = \frac{1}{s} \int_0^\infin f(\tau) e^{-s\tau} d\tau = \frac{F(s)}{s} $$
1.5 微分特性:拉氏变换 n 阶导数公式
1 阶导数
对于 $f(t)$ 的导数,进行拉式变换可以得到:
$$ \mathcal{L}{f{’}(t)} = sF(s) - f(0) $$
证明过程:
从定义出发,
$$ \mathcal{L}{f’(t)}=\int_0^\infin f’(t)e^{-st} dt. $$
做分部积分(取 $u=f(t),\ dv=e^{-st}dt$),得到
$$ \int_0^\infin f’(t)e^{-st}dt=\Big[f(t)e^{-st}\Big]_0^\infin + s\int_0^\infin f(t)e^{-st}dt. $$
在指数衰减条件下 $\lim_{t\to\infin}f(t)e^{-st}=0$,因此边界项为 $-f(0)$。于是
$$ \mathcal{L}{f’(t)}=sF(s)-f(0), $$
成立。
这里提 2 点:
- 有的时候把 $f(0)$ 写成 $f(0^{+})$,指的是 右侧极限,这里是强调是在 $ t > 0 $ 的范围,所以取右侧极限。
- 这里顺便提一下 $f(0)$ 在这里实际上是原函数中的直流分量,因为每求一阶导数,原函数中的常数项就消失了,$F(s)$ 是原函数的拉式变换,如果 $sF(s)$ 能表示导数的拉式变换,就肯定需要把原来的直流分量给去掉。
n 阶导数
对因果函数(因果函数在“系统开始响应之前没有任何输出”),有
$$ \mathcal{L}{f^{(n)}(t)}=s^n F(s)-s^{n-1}f(0)-s^{n-2}f’(0)-\cdots-f^{(n-1)}(0), $$
其中 $F(s)=\mathcal{L}{f(t)}$,且 $f,f’,\dots,f^{(n-1)}$ 在 $t=0^+$ 存在,且 $f$ 为指数阶使积分收敛。
比如对于 2 阶导数
$$ \mathcal{L}{f’’(t)} = s^2 F(s) - s f(0) - f’(0), $$
这个 n 阶的证明过程不在这里写了,通过归纳法可以证明。
1.6 线性性质
拉普拉斯变换是线性的:
$$ \mathcal{L}{a f(t) + b g(t)} = a F(s) + b G(s) $$
其中 $a, b$ 是常数,$F(s) = \mathcal{L}{f(t)}$,$G(s) = \mathcal{L}{g(t)}$。
这意味着我们对每个分量套公式再做线性加减法,完全是可行的。
2. 求解常微分方程
解微分方程:
$$ y’’ + 3y’ + 2y = e^{-t}, \quad y(0) = 0, \quad y’(0) = 0 $$
当然不止一种方法,这里介绍的是如何用拉普拉斯变换来解。
拉普拉斯变换可以把微分运算转换成代数运算,从而把一个微分方程变成一个代数方程。
因为拉普拉斯变换把原来的各种微分,都变成了 $sF(s)$ 所表达这种类似的形式。
2.1 对方程进行拉普拉斯变换
令
$$ \mathcal{L}\left[y(t)\right] = Y(s) $$
根据对导数求拉普拉斯变换的性质:
$$ \mathcal{L}{y’} = sY(s) - y(0) $$
$$ \mathcal{L}{y’’} = s^2 Y(s) - s y(0) - y’(0) $$
代入初值 $y(0)=0, y’(0)=0$:
$$ \mathcal{L}{y’’} = s^2 Y(s) $$
$$ \mathcal{L}{3y’} = 3s Y(s) $$
$$ \mathcal{L}{2y} = 2 Y(s) $$
$$ \mathcal{L}{e^{-t}} = \frac{1}{s+1} $$
所以方程变为:
$$ s^2 Y(s) + 3s Y(s) + 2 Y(s) = \frac{1}{s+1} $$
2.2 求解代数方程
提取 $Y(s)$:
$$ Y(s) (s^2 + 3s + 2) = \frac{1}{s+1} $$
分解因式:
$$ s^2 + 3s + 2 = (s+1)(s+2) $$
所以:
$$ Y(s) = \frac{1}{(s+1)^2 (s+2)} $$
2.3 反拉普拉斯变换
首先进行因式分解,因为拆分后才可以方便套公式直接做反拉普拉斯变换
$$ \frac{1}{(s+1)^2 (s+2)} = \frac{A}{s+1} + \frac{B}{(s+1)^2} + \frac{C}{s+2} $$
两边通分:
$$ 1 = A(s+1)(s+2) + B(s+2) + C(s+1)^2 $$
通过代入 $s=-1, -2$ 或系数比较,求出:
- $s=-1$ → $1 = B(1) \Rightarrow B=1$
- $s=-2$ → $1 = C(1) \Rightarrow C=1$
- 选择 $s=0$ → $1 = A(2) + B(2) + C(1) = 2A + 2 + 1 \Rightarrow 2A = -2 \Rightarrow A=-1$
所以分解为:
$$ Y(s) = \frac{-1}{s+1} + \frac{1}{(s+1)^2} + \frac{1}{s+2} $$
之后,做反拉普拉斯变换:
$$ y(t) = \mathcal{L}^{-1}{Y(s)} = -e^{-t} + t e^{-t} + e^{-2t} = t e^{-t} - e^{-t} + e^{-2t} $$
最终结果:
$$ y(t) = t e^{-t} - e^{-t} + e^{-2t} $$
