本文仅聚焦于如下几个问题:
- 从三角级数展开,过渡到欧拉形式的傅里叶变换
- 什么是离散傅里叶变换
- 什么是2D傅里叶变换
- 从2D傅里叶变换,解释到2D离散傅里叶变换
- 如何对图像进行2D傅里叶变换
- 2D傅里叶变换的周期性问题
- 从2D傅里叶变换的周期性理解傅里叶2D频谱图的中心化
傅里叶级数
傅里叶级数是一种数学工具,它表示一个周期函数为一组正弦和余弦函数的无穷和。
三角级数展开
傅里叶变换最初是基于三角级数展开,即周期函数可以表示为一系列正弦和余弦函数的线性组合:
$$ f(t) = a_0 + \sum_{n=1}^{\infty} a_n \cos(n\omega_0 t) + b_n \sin(n\omega_0 t) $$
其中 $\omega_0 = \frac{2\pi}{T}$ 是基本频率。
复指数形式
利用欧拉公式:
$$ \cos(x) = \frac{e^{ix} + e^{-ix}}{2}, \quad \sin(x) = \frac{e^{ix} - e^{-ix}}{2i} $$
可以将傅里叶级数改写为复指数形式:
$$ f(t) = \sum_{n=-\infty}^{\infty} c_n e^{in\omega_0 t} $$
其中 $c_n$ 是复数系数,封装了正弦和余弦部分的信息。欧拉形式的傅里叶表示更对称、更易于处理,也为后续推广到连续和多维情况提供了基础。
在这里,$n$的取值范围变成了$-\infty$到$\infty$。
离散傅里叶变换 DFT
离散傅里叶变换(Discrete Fourier Transform,简称 DFT)是傅里叶分析的一个重要分支,它的作用是将离散的有限长度信号(通常是数字信号)从时间域/空间域转换到频率域,表示成一组复数频率分量的叠加。
实际中我们处理的是有限、离散的数据。离散傅里叶变换(DFT)定义如下:
$$ X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-i \frac{2\pi}{N}kn}, \quad k = 0, 1, \dots, N-1 $$
对应的逆变换为:
$$ x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] \cdot e^{i \frac{2\pi}{N}kn} $$
DFT 把时间域信号 $x[n]$ 映射到频域 $X[k]$,每个 $X[k]$ 对应一个频率分量的幅度和相位。
负频率、周期重排
离散傅里叶变换中,可以有负频率。
虽然 DFT 的索引 $k$ 是非负整数,但傅里叶频率具有模 $N$ 的周期性。
也就是说:
$$ e^{-j \frac{2\pi}{N} k n} = e^{-j \frac{2\pi}{N} (k + mN) n}, \quad \forall m \in \mathbb{Z} $$
因此,频率 $k = N - 1$ 实际上等价于频率 $-1$,频率 $k = N - 2$ 等价于 $-2$,以此类推。
我们可以将频率索引重新解释为从负频率到正频率:
$$ k = -\frac{N}{2}, \dots, -1, 0, 1, \dots, \frac{N}{2} - 1 \quad (\text{当 } N \text{ 为偶数时}) $$
这种方式可以通过频谱的中心化重排,使得结果更符合频率对称直觉。
在后面的对图像的2D傅里叶变换后,频谱图通过中心化重排后,将低频区域全部变换到中央。
2D傅里叶变换
傅里叶变换可以从将原本的1D形式,扩展到2D形式。
什么是2D傅里叶变换
连续2D傅里叶变换的定义如下,对于一个连续函数 $f(x, y)$:
$$ F(u, v) = \iint_{-\infty}^{\infty} f(x, y) \cdot e^{-i2\pi (ux + vy)} , dx,dy $$
其逆变换为:
$$ f(x, y) = \iint_{-\infty}^{\infty} F(u, v) \cdot e^{i2\pi (ux + vy)} , du,dv $$
其中 $(x, y)$ 是空间域坐标,$(u, v)$ 是频率域坐标。变换结果 $F(u, v)$ 描述了信号中每个频率分量的幅值和相位。
2D 离散傅里叶变换
离散情况下,对于一个 $M \times N$ 的二维离散函数 $f[m, n]$,其二维离散傅里叶变换(2D DFT)定义为:
$$ F[k, l] = \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f[m, n] \cdot e^{-i 2\pi \left( \frac{km}{M} + \frac{ln}{N} \right)} $$
其逆变换为:
$$ f[m, n] = \frac{1}{MN} \sum_{k=0}^{M-1} \sum_{l=0}^{N-1} F[k, l] \cdot e^{i 2\pi \left( \frac{km}{M} + \frac{ln}{N} \right)} $$
2D傅里叶变换的周期性
类似于1D DFT,2D DFT 也具有周期性:
$$ F[k + M, l] = F[k, l], \quad F[k, l + N] = F[k, l] $$
这意味着频谱在两个方向(水平和垂直)上都是周期性的。
DFT 中的频率索引 $k$ 和 $l$ 取值范围是 $0$ 到 $M-1$ 和 $N-1$,但这些索引并不是单纯的“正频率”,它们是模周期的。
因为周期是 $M$ 和 $N$,所以后半部分可以看作对应的负频率分量。具体来说,当索引 $k > \frac{M}{2}$ 时,实际频率等价于 $k - M$ 对应的负频率;同理,当索引 $l > \frac{N}{2}$ 时,频率等价于 $l - N$ 对应的负频率。这样,频率索引的范围在 $[0, M-1]$ 和 $[0, N-1]$ 上循环,形成正负频率对称的结构。
如何对图像进行2D傅里叶变换
Python 中可以使用 numpy 或 opencv 等库方便地进行 2D 傅里叶变换。例如,使用 NumPy:
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
# 加载图像并转换为灰度
img = Image.open('doge.jpg').convert('L')
f = np.array(img)
# 计算2D傅里叶变换
F = np.fft.fft2(f)
# 幅度谱与相位谱
magnitude_spectrum = np.abs(F)
phase_spectrum = np.angle(F)
log_magnitude = np.log(1 + magnitude_spectrum)
# 创建子图
fig, axs = plt.subplots(1, 3, figsize=(15, 5))
# 原始图像
axs[0].imshow(f, cmap='gray')
axs[0].set_title('Original Image')
axs[0].axis('off')
# 幅度谱
axs[1].imshow(log_magnitude, cmap='gray')
axs[1].set_title('Magnitude Spectrum (log)')
axs[1].axis('off')
# 相位谱
im = axs[2].imshow(phase_spectrum, cmap='gray')
axs[2].set_title('Phase Spectrum')
axs[2].axis('off')
# 添加 colorbar 到相位谱
fig.colorbar(im, ax=axs[2], shrink=0.7)
plt.tight_layout()
plt.show()
运行后可以看到幅度谱和相位谱,这里需要注意的一点在于,

逆变换还原图像(频率+相位)
傅里叶变换的结果是复数,包含了幅度(Magnitude)和相位(Phase)信息。只保留其中之一就不能完整还原图像。
还原图像的方式如下:
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
# 加载图像并转换为灰度
img = Image.open('doge.jpg').convert('L')
f = np.array(img)
# 计算2D傅里叶变换
F = np.fft.fft2(f)
# 进行逆傅里叶变换
recovered = np.fft.ifft2(F)
recovered_real = np.real(recovered)
plt.imshow(recovered_real, cmap='gray')
plt.title('Recovered Image from IFFT')
plt.axis('off')
plt.show()
逆变换后应该和原图一样。

频谱图中心化
为了更清晰地观察频率分布,我们通常对频谱进行中心化,使低频位于中心,高频分布在周围。
中心化操作可以使用 np.fft.fftshift:
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('doge.jpg', cv2.IMREAD_GRAYSCALE)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
magnitude_spectrum = 20 * np.log(np.abs(fshift) + 1)
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.title('Original Image')
plt.imshow(img, cmap='gray')
plt.subplot(1, 2, 2)
plt.title('Magnitude Spectrum')
plt.imshow(magnitude_spectrum, cmap='gray')
plt.show()
此时频谱图将低频成分移到了中心,更易于观察纹理和方向性等信息。
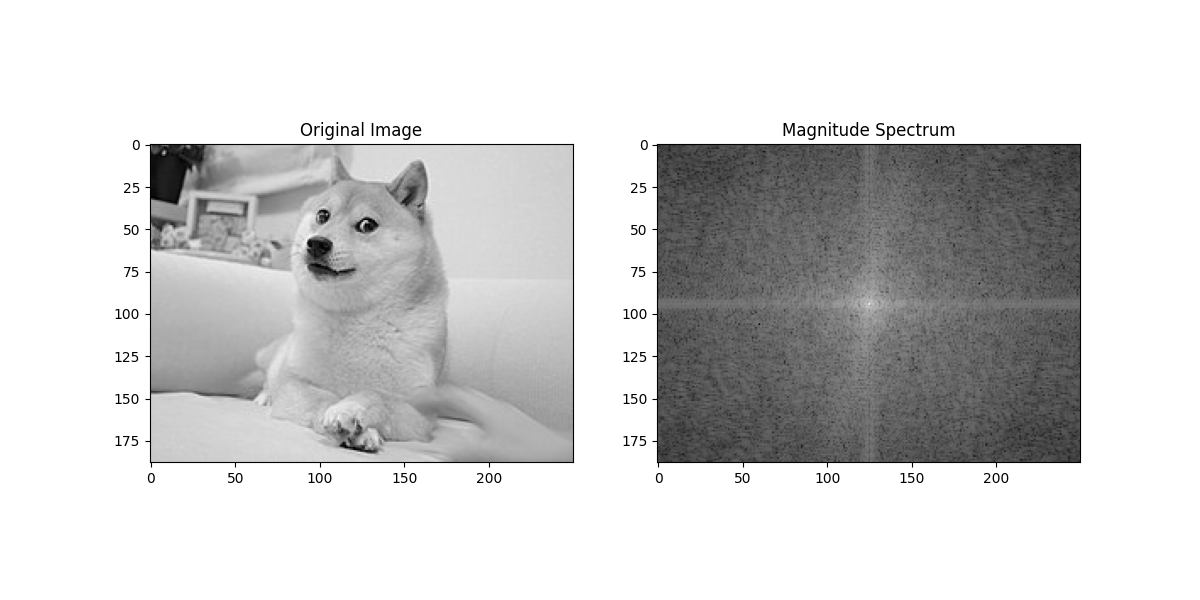
中心大致可以表示轮廓信息,而细节纹理是高频信息位于边缘。
